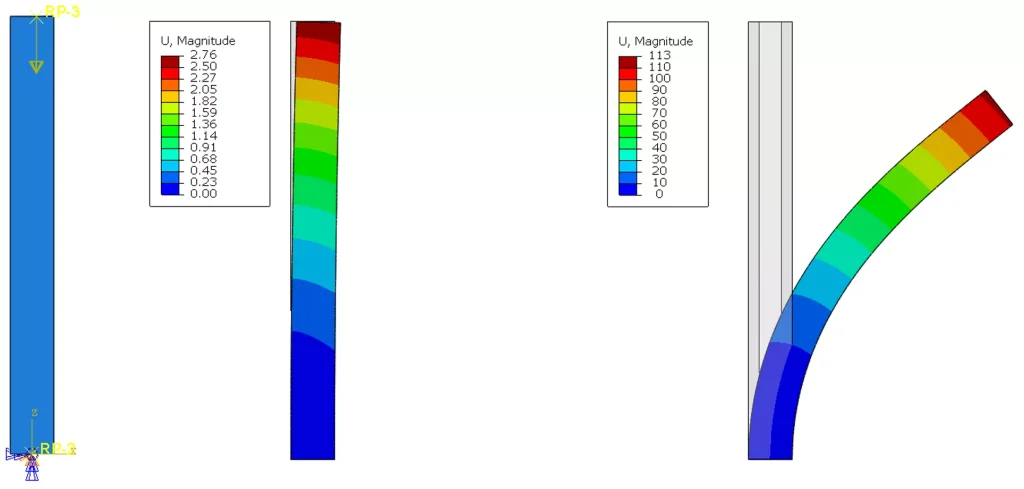
Understanding When and Why Nonlinear Analysis Is Required
Introduction
Finite Element Analysis (FEA) is a fundamental tool in modern engineering design, enabling engineers to predict structural behavior, optimize performance, and reduce physical prototyping costs. While many early-stage simulations rely on linear FEA, real-world engineering problems often involve complexities that linear assumptions cannot capture.
Choosing between linear vs nonlinear FEA is not simply a matter of software capability—it directly affects the accuracy, reliability, and safety of engineering decisions. Misapplying linear analysis to nonlinear problems can result in underestimated stresses, incorrect deformation predictions, and unsafe designs.
This article provides a technical comparison of linear and nonlinear FEA, explains what nonlinear FEA is, and clarifies when to use nonlinear FEA based on physical behavior, material response, and boundary conditions. It is written for engineers, analysts, and engineering managers seeking accurate and defensible simulation results.
What Is Linear FEA?
Linear FEA assumes a proportional relationship between applied loads and structural response. In other words, if the load doubles, stresses and displacements also double.
Core Assumptions of Linear FEA
Linear analysis relies on three key assumptions:
Linear material behavior
Stress is proportional to strain (Hooke’s Law)
No yielding, plasticity, or damage
Small deformations
Geometry does not significantly change during loading
Stiffness remains constant
Linear boundary conditions
Loads and constraints do not change with deformation
When these assumptions hold, linear FEA provides fast, stable, and computationally efficient results.
Advantages of Linear FEA
Low computational cost
Fast solution times
Easy model setup and convergence
Suitable for early design stages
Ideal for stiffness-based comparisons
Linear FEA is commonly used for:
Initial sizing of components
Elastic stress checks
Design optimization iterations
Low-load structural analysis
However, its simplicity becomes a limitation when real-world nonlinearities are present.
Limitations of Linear FEA
Linear FEA cannot accurately represent:
Plastic deformation
Large displacements or rotations
Contact interactions
Material failure
Buckling beyond critical load
Using linear analysis in such cases may lead to non-conservative or misleading results, especially in safety-critical applications.
What Is Nonlinear FEA?
Nonlinear FEA accounts for conditions where the relationship between load and response is no longer proportional. In nonlinear analysis, stiffness changes during the solution process, requiring incremental and iterative solving methods.
Key Characteristics of Nonlinear FEA
Load is applied incrementally
System stiffness is updated continuously
Equilibrium is solved iteratively
Convergence criteria must be satisfied
Nonlinear FEA is essential when any assumption of linearity is violated.
Types of Nonlinearity in FEA
1. Material Nonlinearity
Occurs when material behavior deviates from linear elasticity.
Examples:
Plastic deformation of metals
Hyperelastic behavior of rubber
Viscoelastic materials
Creep and time-dependent effects
Material nonlinear FEA is critical for:
Failure prediction
Residual stress analysis
Crash and impact simulations
2. Geometric Nonlinearity
Occurs when deformations are large enough to affect the structure’s stiffness.
Examples:
Large deflections
Large rotations
Buckling and post-buckling behavior
Geometric nonlinearity is common in:
Thin-walled structures
Slender beams and columns
Membranes and cables
3. Contact Nonlinearity
Occurs when parts interact, separate, or slide against each other.
Examples:
Assembly simulations
Bolted and press-fit joints
Gear contacts
Seals and gaskets
Contact problems are inherently nonlinear because contact conditions change during loading.
Linear vs Nonlinear Analysis: Key Differences
Mathematical Behavior
| Aspect | Linear FEA | Nonlinear FEA |
|---|---|---|
| Load-response | Proportional | Non-proportional |
| Stiffness | Constant | Variable |
| Solution | Single step | Incremental & iterative |
| Convergence | Guaranteed | Must be checked |
Accuracy and Applicability
Linear analysis provides approximate solutions under ideal assumptions, while nonlinear analysis provides physically realistic results for complex behaviors.
However, nonlinear FEA requires:
More setup effort
Higher computational cost
Expert interpretation
When to Use Nonlinear FEA
Understanding when to use nonlinear FEA is crucial for engineering accuracy and safety.
Use Nonlinear FEA When:
Stress exceeds elastic limits
Permanent deformation is expected
Large displacements occur
Contact or separation exists
Buckling or collapse is possible
Material behavior is nonlinear
Typical Applications of Nonlinear FEA
Plastic forming processes
Structural collapse analysis
Impact and crash simulations
Rubber and elastomer components
Bolted joint behavior
Pressure vessels beyond elastic range
Common Engineering Mistakes in FEA Selection
Mistake 1: Using Linear FEA for Plastic Behavior
Linear FEA cannot predict:
Yielding
Residual stress
Permanent deformation
This often leads to unsafe underestimation of failure risk.
Mistake 2: Ignoring Geometric Nonlinearity
In slender or flexible structures, ignoring large deflections can:
Overestimate stiffness
Misrepresent load paths
Miss buckling behavior
Mistake 3: Oversimplifying Contact Conditions
Replacing contact with fixed constraints may:
Artificially stiffen the model
Produce unrealistic stress concentrations
Computational Cost: Linear vs Nonlinear FEA
Linear FEA:
Fast
Low memory usage
Suitable for optimization loops
Nonlinear FEA:
High computational cost
Requires solver tuning
Sensitive to mesh quality and time step size
Engineering judgment is essential to balance accuracy vs efficiency.
Validation and Verification in Nonlinear FEA
Nonlinear results must be carefully validated using:
Mesh convergence studies
Sensitivity analysis
Experimental correlation
Energy balance checks
Without proper validation, nonlinear simulations can be misleading despite their complexity.
The Role of Engineering Consulting in Advanced FEA
Advanced FEA requires:
Deep understanding of mechanics
Numerical methods expertise
Industry-specific experience
Engineering consulting firms help:
Select appropriate analysis type
Define realistic assumptions
Interpret nonlinear results correctly
Reduce risk in critical designs
At Avesta Consulting, both linear and nonlinear FEA are applied strategically to ensure accuracy, safety, and cost efficiency across industrial projects.
Conclusion
Understanding the differences between linear vs nonlinear FEA is essential for reliable engineering simulation. Linear FEA is efficient and valuable for elastic, small-deformation problems, but it becomes insufficient when real-world nonlinearities are present.
Nonlinear FEA captures material behavior, large deformations, and contact effects, making it indispensable for advanced engineering analysis. Knowing when to use nonlinear FEA ensures accurate predictions, safer designs, and better engineering decisions.
Choosing the correct analysis approach is not just a numerical decision—it is a critical engineering responsibility.